In the tests below the test set will serve more as a validation test than a real test set (which we must not touch during the training)

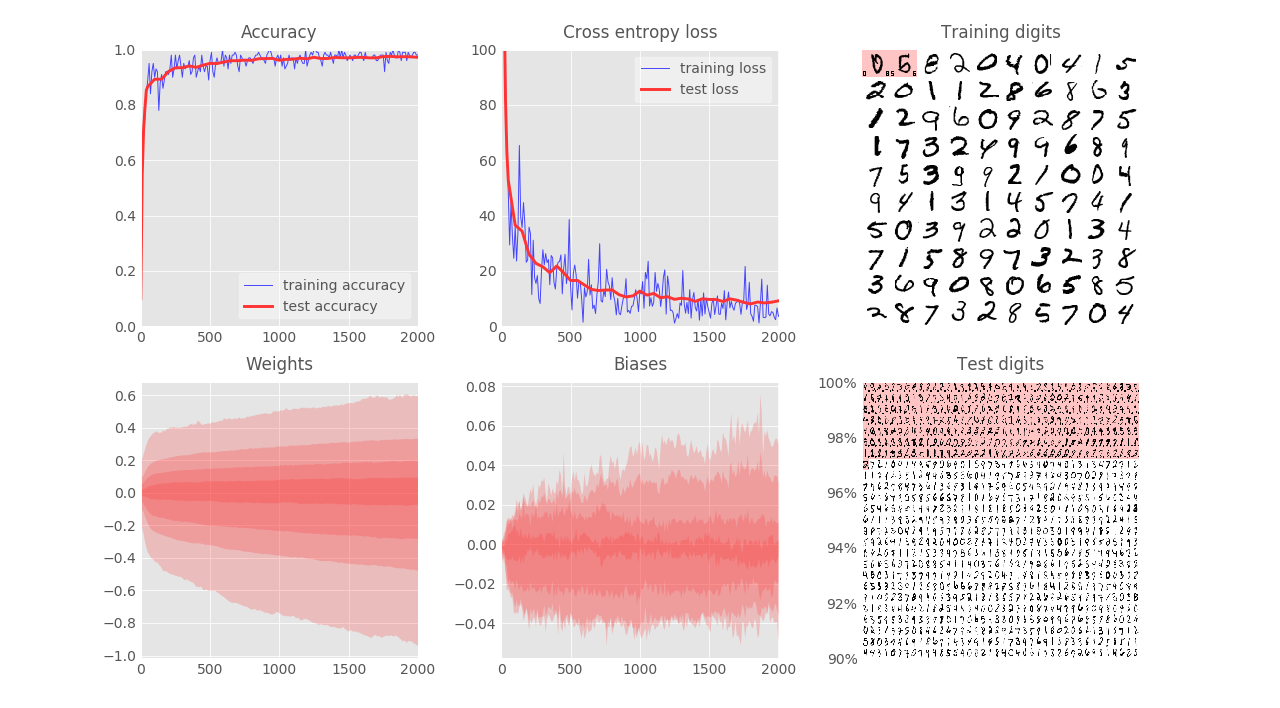
1. No hidden layer

  • (28x28x1) – (10)
  • weights (784x10) and bias (10) both initialized at $0$
  • (Stochastic) Gradient Descent with learning rate = $0.5\%$ for batch $100$

Result:

  • Print training loss and accuracy as well as testing loss and accuracy
  • Get test accuracy $92\%$ after $2000$ iterations

Comment: Not usable in production (imagine detecting zip code application)

Test with other parameters

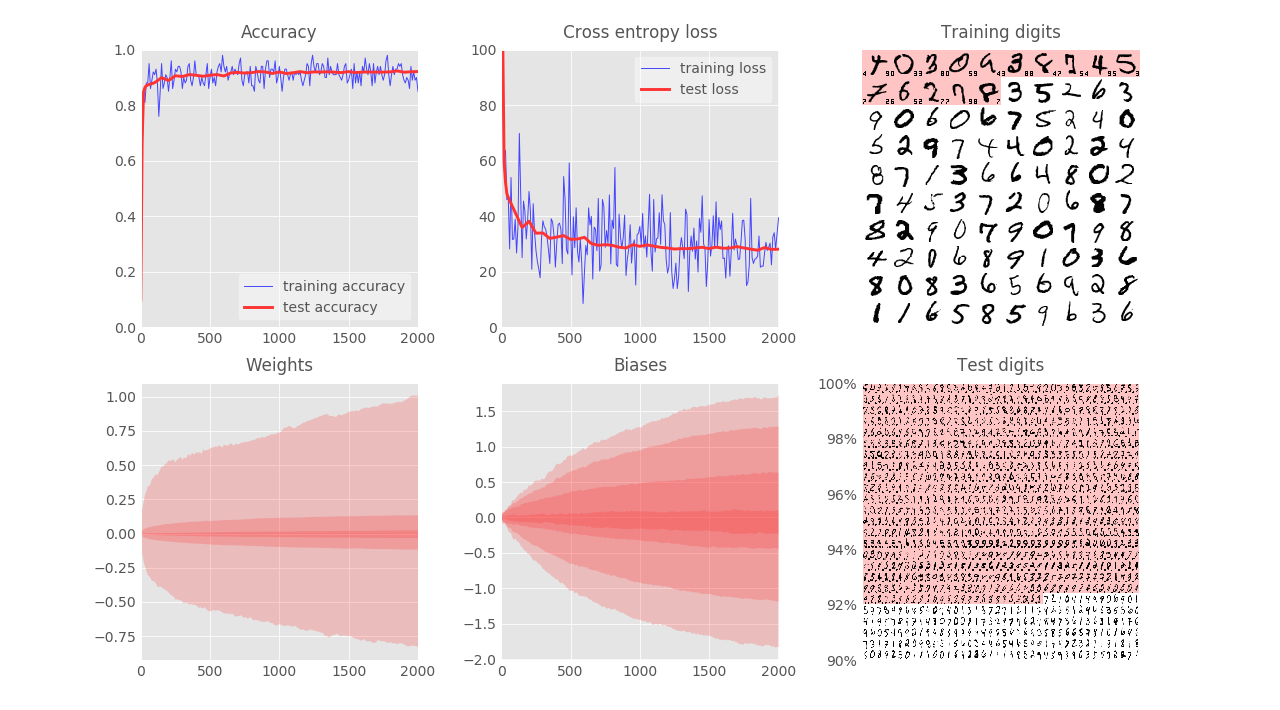
  • learning rate = $1\%$ ==> quite similar result, but the loss function fluctuates more.
  • learning rate = $2\%$ ==> explosion
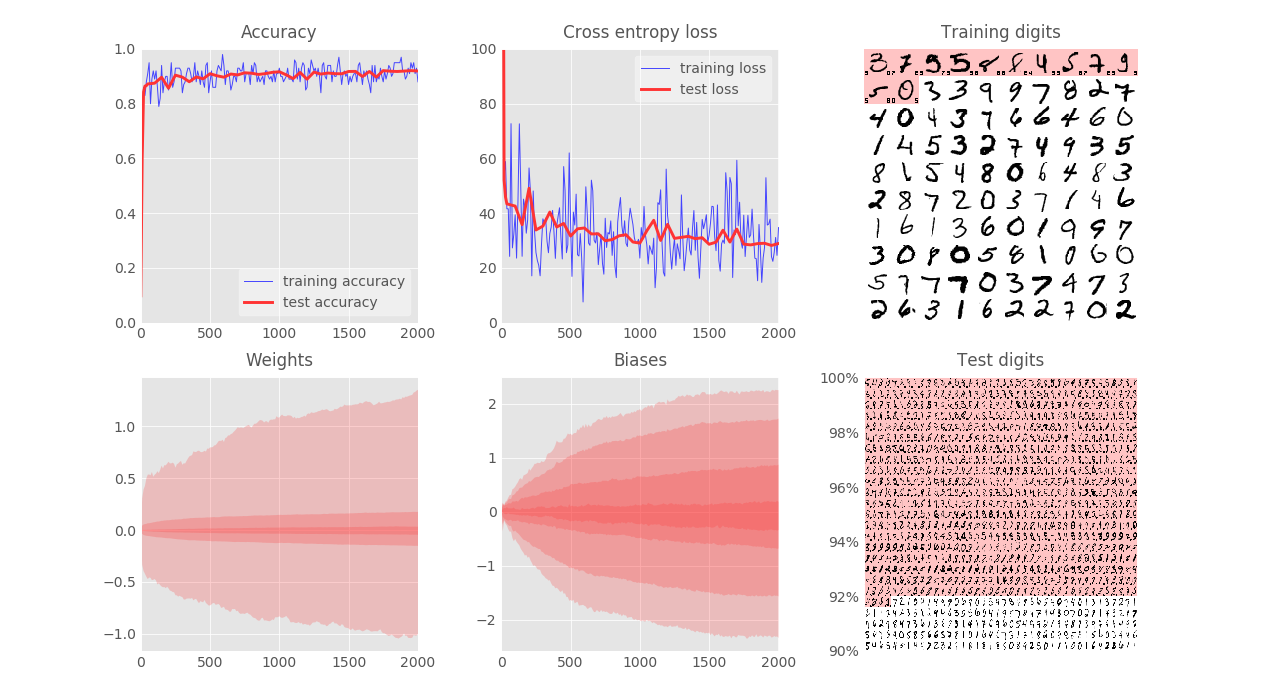
  • learning rate = $0.1\%$ ==> converge slower but smoother, (test accuracy reaches $91.5\%$ after $2000$ iterations)

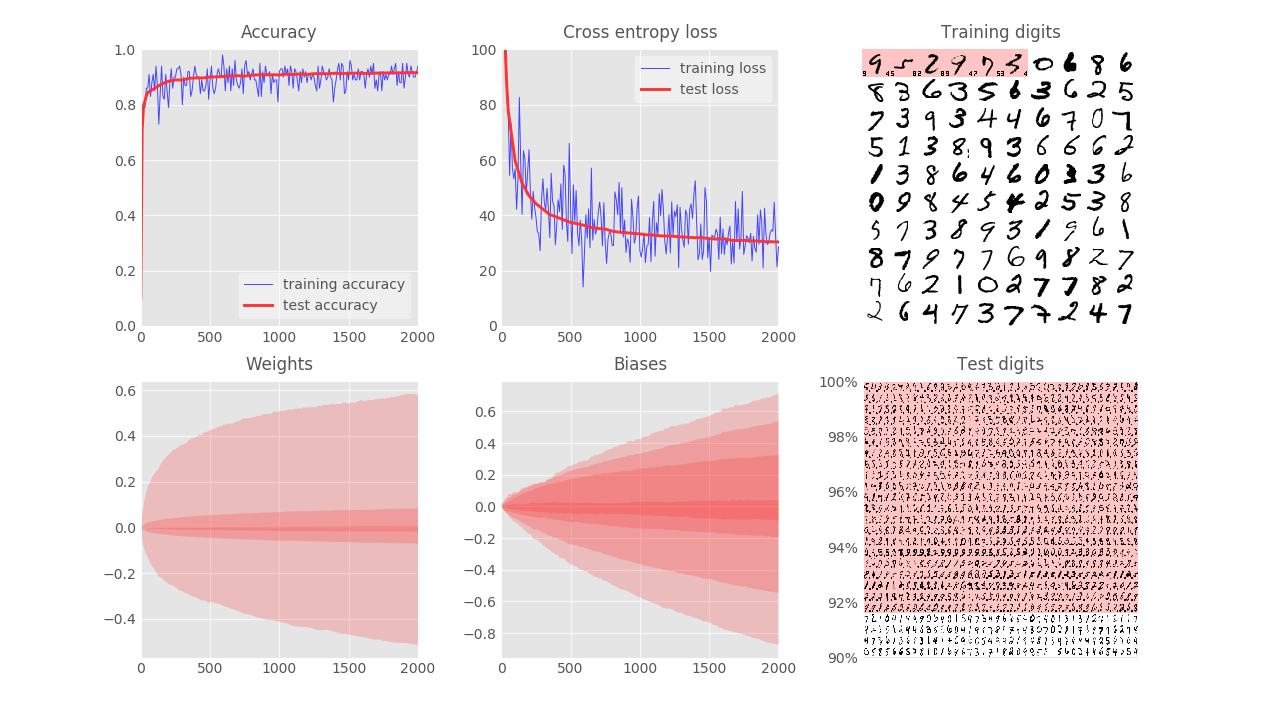
2. Two hidden layers

  • (28x28x1) – (200) – (100) – (10)
  • weights (784x200), (200x100), (100x10) initialized using truncated_normal with std = 0.1
  • bias are all initialized at 0
  • sigmoid activation
  • (Stochastic) Gradient Descent with learning rate = $0.5\%$ for batch $100$

Result:

  • Test accuracy (which means validation accuracy in this post) reaches $94.3\%$ after $2000$ iterations:

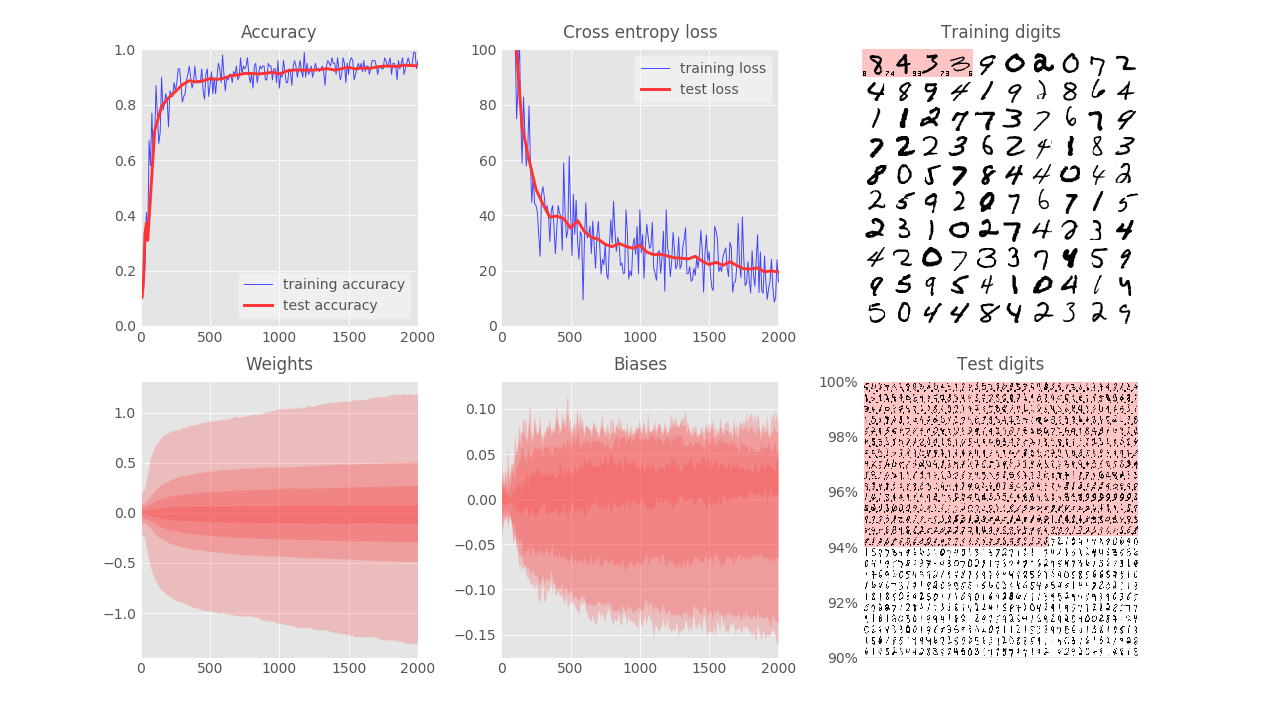
Weight initialization:

  • Modify the weights initialization with std = 1: the convergence is worse ($91.3\%$). This reconfirms the importance of weights initialization.

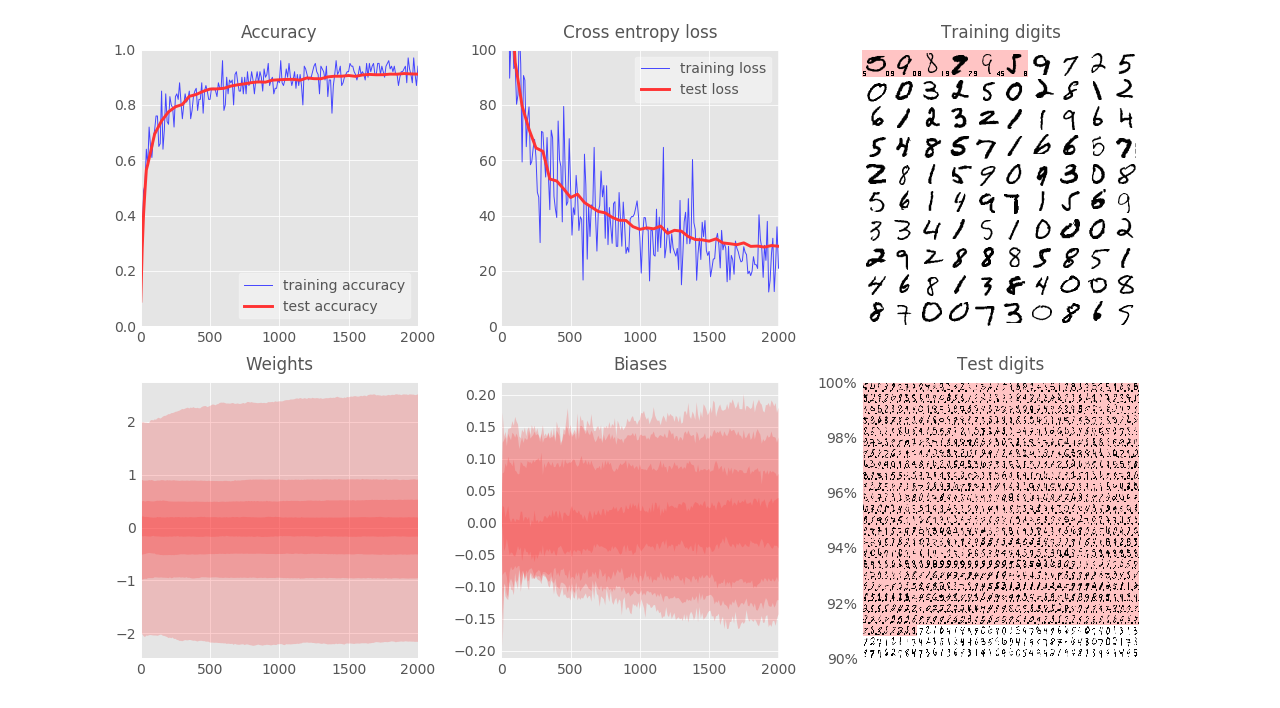
Note that the Xavier initialization is $var(W) = 1/N_{in}$ so with our numbers of input = 784, 200, 100 for each layer, the first std = 0.1 is more or less the Xavier initialization.

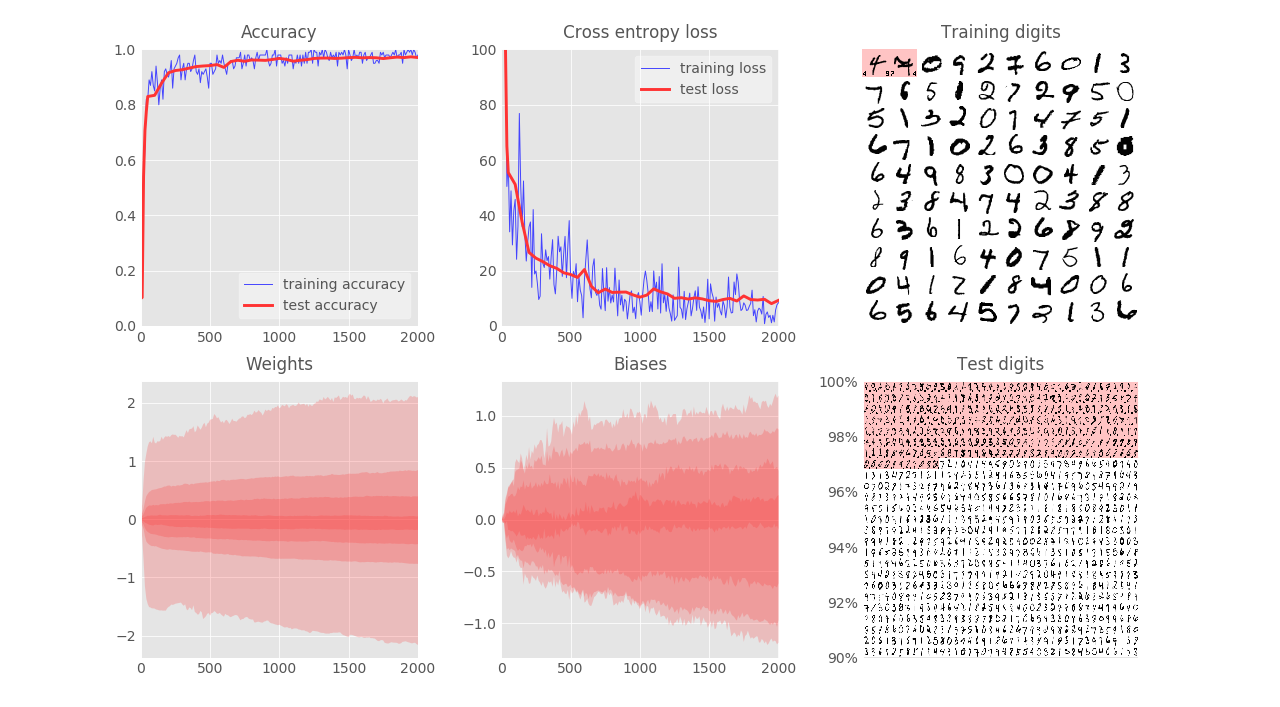
Optimizer:

  • Use MomentumOtimizer with the same learning rate = $0.5\%$ and momentum=$0.9$, the convergence is much faster than SGD and the (test) validation accuracy reaches $97.3\%$ after $2000$ iterations:

  • Use AdamOptimizer with the same learning rate = $0.5\%$, the convergence is much faster than SGD and the (test) validation accuracy reaches $97.5\%$ after $2000$ iterations: